«Природа устремлена к безграничному. Всем
без исключения большим и прекрасным, что
заключено в конечных силах, стремится она
овладеть, объединив их в целое».
© Вильгельм фон Гумбольдт «О различии между полами и его
влиянии на органическую природу»
Полудождливым сентябрьским субботним днём случилось то, чего мы довольно давно задумывали сделать. Прошёл первый — и есть все основания считать, что первый в мире! — физико-математический биатлон среди старшеклассников нашего славного города. Каковой и дал старт набору в Красноярскую летнюю школу сезона 2013 года.
Физико-математический биатлон — командная эстафета. Побеждает та команда (из
Здесь надо сделать одно важное отступление. Есть в русском интернете такая народная забава — клясть почём зря чиновников всех уровней и мастей. Так вот, вопреки этой забаве, очень хочется сказать слава благодарности именно чиновникам! Идею проведения физ-мат биатлона очень активно поддержали именно эти самые чиновники, которых принято ругать со специальным сладострастием. Главное управление по физической культуре, спорту и туризму администрации Красноярска не просто поддержало эту идею организационно — составление и подписание необходимых бумаг, распространение информации по школам, сбор команд, место проведения предоставили, — но и лично активно приняли участие в проведении биатлона. За что им хочется сказать большое спасибо!
Вот как выглядит статистика по участникам. Повторюсь, предполагалось, что каждый район города выставит три сборные: две мужских и одну женскую. По факту команды представляли не район, а школы. Лидерами среди школ по числу команд явились гимназия № 1 «Универс» и лицей № 7 — они выставили по три команды каждая! При этом следует сказать особенные слова в адрес учеников (и, главным образом, учениц) седьмого лицея — эти команды были собраны при их активнейшем участии и по их инициативе. Что радует!
По районам расклад получился такой (число мужских/женских команд): Железнодорожный — одна школа (2/1), Кировский — три школы (2/1), Ленинский — три школы (2/1), Октябрьский — четыре школы (4/3), Свердловский — три школы (2/1), Советский — одна школа (1/1), Центральный — две школы (2/1).
Надо отдать должное участникам биатлона: все они с известным энтузиазмом отнеслись к поставленной задаче. Увы, поскольку первый биатлон организовывался до определённой степени впопыхах, постольку не все команды оказались одинаково готовыми к этому соревнованию. Некоторые команды выставили специалистов лишь в одном предмете (в математике; физика нынче не в почёте), некоторые решили специализироваться на беге. И тем не менее, азарт захватил всех: все бились изо всех сил. О том свидетельствует хотя бы тот факт, что члены одной команды искренно пытались подсказать друг другу решения задач. Что, в общем, было скорее вредным: списывание, как известно, приводит лишь к увеличению числа ошибок...
Третье место среди юношей заняла команда школы № 135 (Кировский район); у девушек третье место заняла команда лицея № 2. Школа № 145 Красноярска (это Советский район) хорошо известна в городе; главный её конёк — это очень хорошо поставленное химическое образование. В этом направлении она в городе вне конкуренции, среди её учеников много олимпиадников всероссийского уровня, и даже международников. С физикой и математикой там не так всё здорово, но всё равно очень хорошо: обе команды этой школы (и мужская, и женская) заняли вторые места в биатлоне.
Наконец, первые места заняли команды второго (Центральный район) и третьего (Ленинский район) лицеев, соответственно, в мужском и женском зачётах. Прямо нумерология какая-то! Все члены этих команд получили приглашение в Красноярскую летнюю школу; они были самыми первыми учениками, зачисленными в неё в сезоне 2013 года! С большим удовольствием назову этих победителей: Игорь Емельянов, Андрей Кононов, Артём Хаиров и Андрей Хохлов победили в интеллектуальном биатлоне 2012 года среди юношей. У девушек победительницами стали Полина Комарова, Маргарита Кулаченко, Елена Лунева и Ирина Михина. Наши поздравления всем этим героям формулы и расчёта! И героиням тоже...
В заключение — задачи, которые предлагались школьникам на биатлоне. Сегодня будет «юношеская порция» (те задачи, которые решали юноши), по математике и физике. Решайте их так: сядьте и сосредоточьтесь на 10 минут. Если вы решили все три задачи по одному предмету не больше, чем за 10 минут — вы можете защищать честь того района, в котором проживаете; если нет, то наложите на себя епитимью столько раз, сколько задач вы не решили...
- Можно ли в выражении ШЕ × СТЬ + 1 = СЕ × МЬ заменить буквы цифрами так, чтобы равенство оказалось верным? Разным буквам соответствуют разные цифры, одной и той же букве — одна цифра. Ответ, ясен пень, обосновать; крестик в середине означает умножение.
- Разность двух целых чисел n и m умножили на их произведение. Может ли в результате получиться число 2012? Ответ, ясен пень, обосновать.
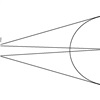
- На плоскости лежат две не пересекающиеся окружности О1 и О2 с радиусами R1 и R2, соответственно. Из центра окружности О1 проведены касательные к окружности О2, а из центра О2 — две прямые, проходящие через точки A и B пересечения касательных с окружностью О1. Чему равна площадь четырёхугольника O1AO2B? (см. рисунок Задача №1)
- Участник городского биатлона первый круг пробежал со скоростью 12 км/час, а второй — со скоростью всего 4 км/час. Чему была равна средняя скорость участника на его этапе? Перерыв между этапами не учитывать.
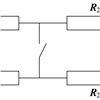
- В электрической цепи (см. рисунок Задача №2) в первом случае ток пропускают из точки A в точку B с замкнутым выключателем, а второй раз — с разомкнутым. Напряжение между точками A и B постоянно. В каком случае — в первом или во втором — полный ток через систему будет больше и во сколько раз? Значения сопротивлений указаны на рисунке.
- С наклонной горки высоты h соскальзывает брусок массы m и проходит расстояние l по горизонтальной поверхности, после чего останавливается. Какую работу надо затратить, чтобы втащить брусок на прежнее место? Трение между бруском и всеми поверхностями равно μ.
Михаил Садовский
Фото Олега Финогенова