«Как много, однако, существует такого, в
чём я не нуждаюсь.»
Сократ
Вспомнил я тут прошлый раз про рекламу, а она тут как тут: иду домой, вынимаю из почтового ящика АПМ (агитационно-пропагандистский материал, если кто не в курсе) — газетёнку «Справедливый край». Ясен пень, по названию — предвыборное агитационное издание «Справедливой России». Даже беглого взгляда на эту газетку достаточно для того, чтобы возникло сильное желание назвать её «Наш справедливый край»... Полистал я ту газетку, полистал и вспомнил, что несколько лет назад сделали мы на пару с А.А.Глисковым работу по моделированию электорального поведения. По-русски сказать, небольшое исследование на тему «Как надо правильно понимать итоги выборов». Как мне кажется, весьма актуальная в настоящий момент работа.
Итак, кратко суть её состоит в следующем. Пусть у вас имеется N кандидатов (партий, объединений, лиц неопределённой физической наружности и т.п.), и избиратели за них голосуют по принципу «один избиратель — один голос». Итоги выборов упорядочивают наших кандидатов по числу поданных за них голосов, и дальнейшее (с точки зрения сделанной научной работы) нас не будет интересовать. Хотя с точки зрения прикладной понятно, что чем больше голосов, тем лучше.
Итак, в ходе выборов мы получаем некоторое распределение голосов: p1 за первого (первого по числу набранных голосов), p2 — за второго и так далее до pN при условии, что p1 + p2 + p3 + ... + pN = 1. Спрашивается: что именно в настроении избирателей отражает наблюдаемое распределение? Для ответа на этот вопрос предложим специальную модельную ситуацию: пусть все N кандидатов избирателям одинаково неизвестны и безразличны; то есть, наши гипотетические избиратели попали в трудную ситуацию: выбор сделать надо, но никаких рациональных оснований (да и иррациональных тоже) нету. Они нам (как избирателям) все равнодушны. Спрашивается, какое распределение голосов {p1, p2, p3, ..., pN} следует ожидать в таком случае?
Соображения типа здравого смысла подсказывают, что в ситуации полного безразличия избирателей к кандидатам голоса должны будут распределиться примерно поровну. И чем больше избирателей приняло участие в голосовании, чем точнее должно быть ожидаемое равенство голосов.
Вся сложность, однако, в том, что человек обладает рефлексией. И поэтому совершенно не способен имитировать по-настоящему случайное поведение. Как показал В.А.Лефевр, распределение голосов в ситуации безразличного выбора для случая двух кандидатов будет подчиняться соотношению, определяемому золотой пропорцией: 0,62... ÷ 0,38... Напомню, что золотая пропорция — это часто используемое человечеством отношение двух величин; в частности, знаменитый Парфенон в Афинах построен целиком на этом отношении. Два отрезка A и B находятся в отношении золотой пропорции, если длина A относится к длине B так же, как длина B относится к длине A + B.
Следовательно, отношения двух «соседних» кандидатов по числу голосов для любой пары должно быть всегда примерно отношением золотой пропорции. Это значит, что в целом последовательность долей голосов будет описываться (убывающей) геометрической прогрессией со знаменателем φ-1, где φ и есть ровно то самое отношение золотой пропорции (для зануд, которые любят в комментариях вечно всё поправлять и уточнять: оно же и золотое сечение. Спасибо вам за помощь и поддержку!). На самом деле, геометрическая прогрессия с таким показателем очень точно описывается последовательностью чисел Фибоначчи, но это для нас сейчас несущественно.
Вернёмся к выборам. Итак, если избиратели голосуют за кандидатов (партии, etc.) в ситуации полной неопределённости, то доли голосов должны убывать в геометрической прогрессии со знаменателем φ-1. Эта теория ничего не говорит (и не должна) о том, как стать первым в этом списке. Или даже вторым. Более того, совершенно не верна противоположная «теорема»: если голоса распределились близко к геометрической последовательности со знаменателем φ-1, то мы имеем дело с ситуацией полного безразличия избирателей. Дело в том, что такое распределение могут давать самые разные факторы (и их совместное действие), а не только безразличный выбор.
Тем не менее, результаты всяких выборов надо анализировать, исходя из того, что «равновесным» распределением является геометрическая последовательность со знаменателем φ-1, а не равномерное распределение (как бы того ни хотелось проигравшим). Вот несколько примеров.
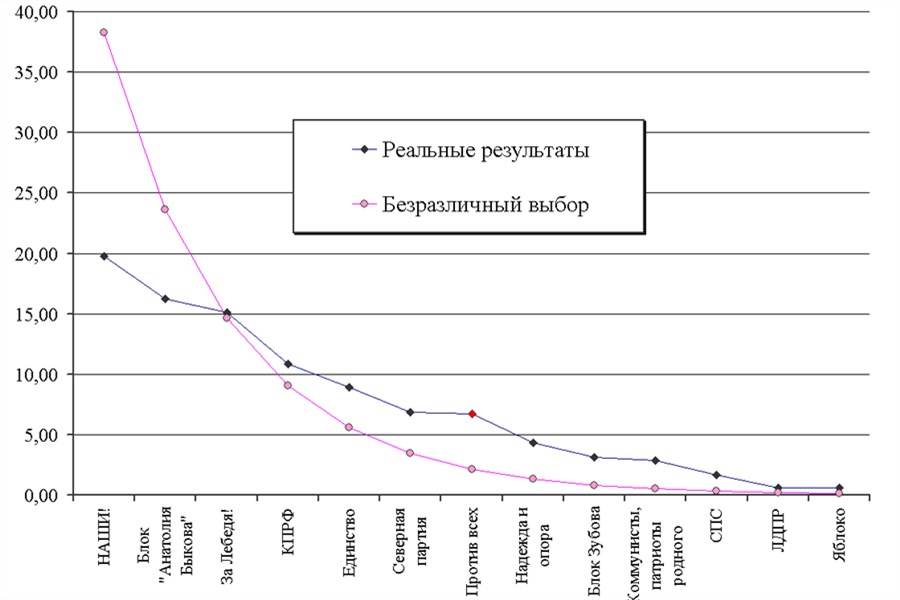
Выборы в Законодательное собрание нашего края 2001 года. Хорошо видно, что лидеры заметно уступают «безразличию» избирателей. Это яркий пример выборов с сильнейшим электоральным напряжением: многие ещё помнят те времена. При этом обратим внимание на то, что, несмотря на наличие одного общего (и мощного) политического конкурента — движения «За Лебедя» — у этих двух лидеров, они, по сути, конкурировали друг с другом. Предвосхищая вопросы, сразу же оговорюсь, что совершенно недопустимо просто складывать голоса избирателей «Наших» и блока А.Быкова: поведение избирателей в ситуации отсутствия одного из них могло быть кардинально другим.
Кроме того, хорошо видно, что все остальные партии «пограбили» лидеров: их рейтинги превышают уровень безразличия. Это неудивительно: в реальности никакая партия не ведёт выборы так, чтобы оставить избирателя в неведении относительно себя самой или безразличным. Хотя партии «Яблоко» это почти удалось...
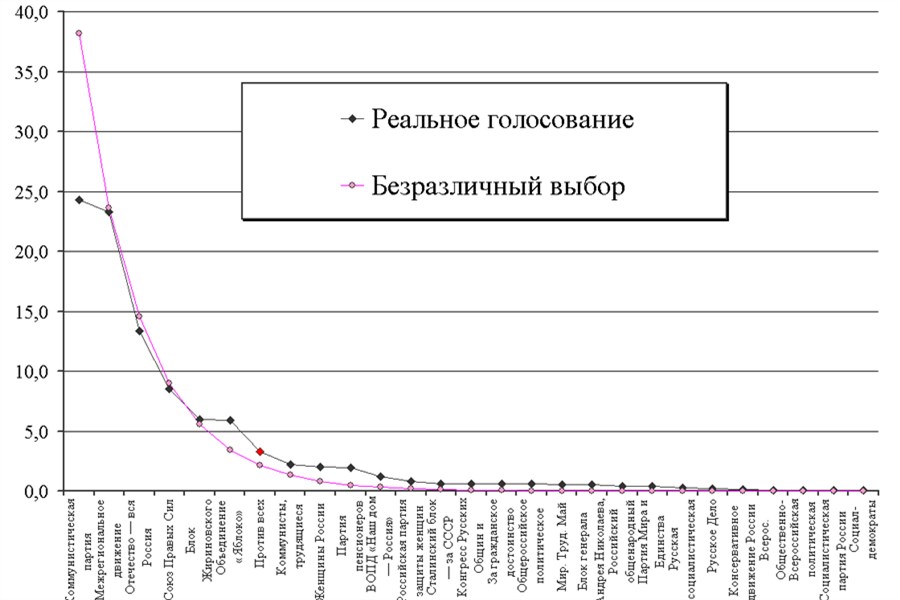
Выборы в ГД ФС РФ 1999 года. Последний успех «Яблока»: они победили кандидата «Против всех». Видно, что «Медведи» и коммунисты были главными соперниками, и борьба тогда тоже была нешуточная.
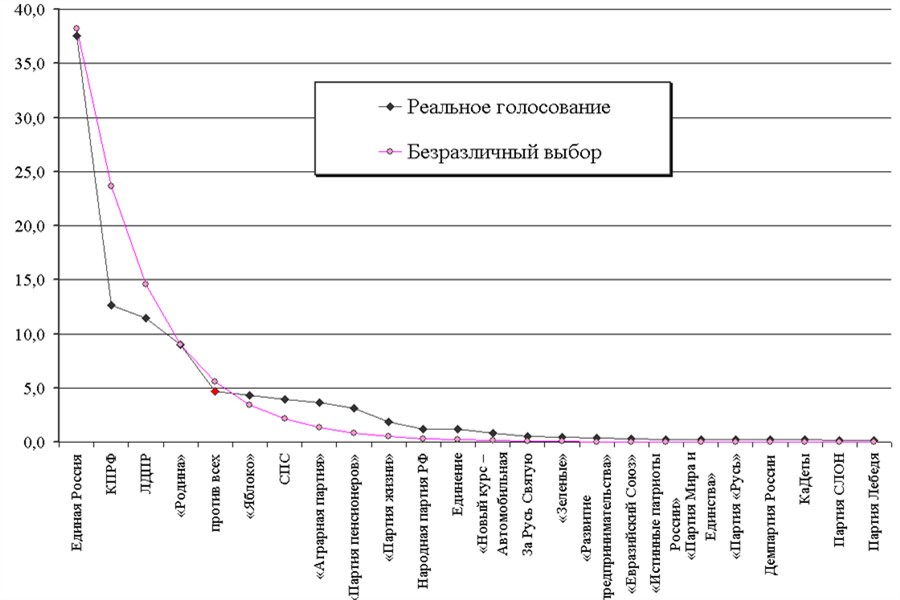
Выборы в ГД ФС РФ 2003 года. Выводы делайте сами.
А теперь — небольшая лотерея.
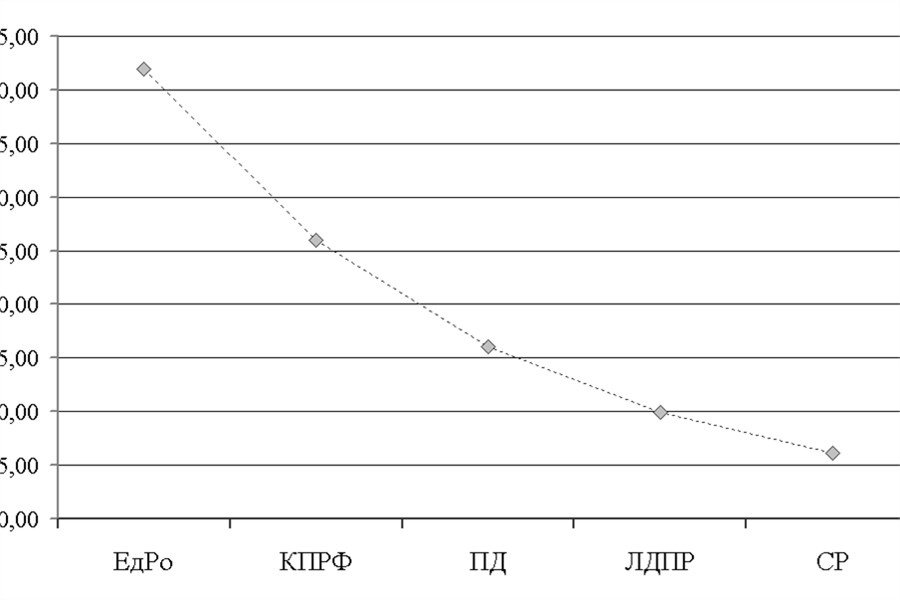
На рисунке показано распределение голосов в ситуации безразличного выбора для предстоящих выборов в наше Законодательное собрание. Порядок партий (по числу набранных голосов) мне лично представляется именно таким. А теперь — рисуют все! Желающие строят график реальных голосов и присылают их в редакцию. Срок сбора прогнозов — до 18-го ноября. А победителю — скромный, но ценный подарок...
Будем считать, что это соревнование нынче проходит у нас по разряду задачек.
Михаил Садовский